
В математике существует много, на первый взгляд, необычных задач. Среди них выделяется задача о перемещении дивана, которая впервые появилась в 1966 году. Это математическая задача, которая является двумерным моделированием реальной житейской проблемы с перемещением дивана в квартире или доме.
Задача состоит в поиске двумерной формы дивана максимальной площади, который можно переместить через коридор в виде буквы Г, каждая часть которого имеет заданную ширину в единицу измерения и сходится под прямым углом. Значение максимальной площади дивана получило название «константа дивана». Теперь математик из Южной Кореи нашел решение этой задачи и свои результаты опубликовал на сервере препринтов ArXiv, пишет Live Science.
Задача о перемещении дивана описывает самый большой диван, который может поместиться в коридоре, состоящем из двух частей, которые сходятся под прямым углом. Действительно, в реальной жизни переместить обычный диван в таком коридоре было бы чрезвычайно сложно, но эта задача предусматривает не совсем обычную форму дивана, которая позволяет это сделать.
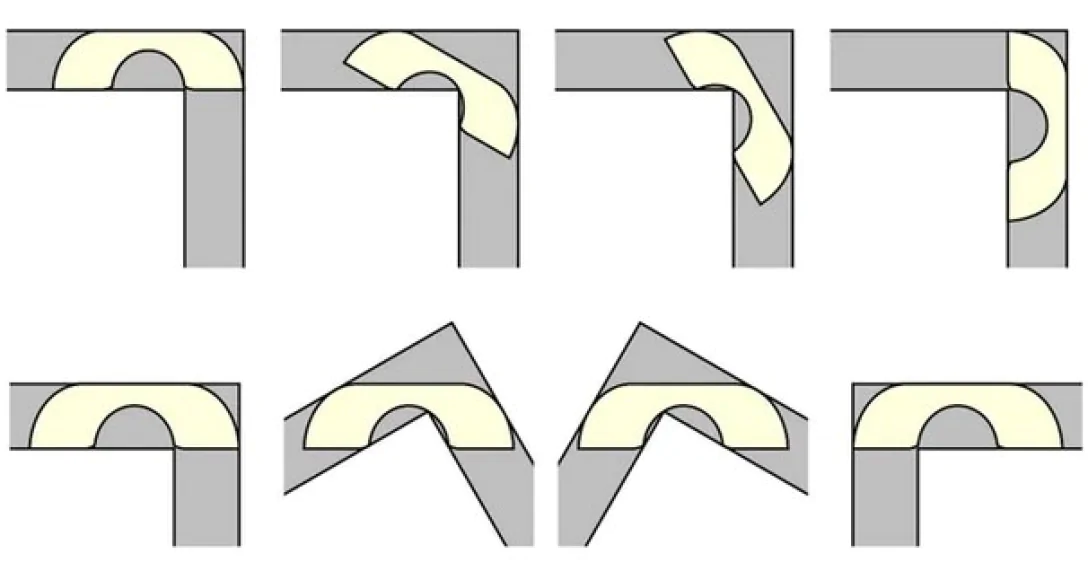
Задачу о перемещении дивана сформулировал в 1966 году канадский математик Лео Мозер. Он предложил найти самую большую возможную площадь одной фигуры в одной плоскости, которая могла бы двигаться вокруг прямого угла коридора с заданной шириной в единицу измерения. Это достаточно сложно, ведь задача включает как вычисление максимальной площади, так и движение фигуры.
Теперь Джинеон Бэк из Университета Енсе в Южной Корее, нашел решение этой задачи. Он представил более чем 100 страниц математических доказательств в своем исследовании. Математик обнаружил, что для коридора шириной в 1 единицу максимальная площадь воображаемого дивана может составлять 2,2195 единиц. То есть это и есть та самая «константа дивана». Таким образом математик представил более точное решение задачи, которое ранее находилось в диапазоне от 2,2195 до 2,37 единиц. Это решение задачи о перемещении дивана еще не прошло экспертную оценку научного сообщества, ведь другие ученые должны подтвердить, что это оптимальное решение.
В 1992 году математик Джозеф Гервер из Ратгерского университета установил нижнюю границу для «константы дивана» на уровне 2,2195 единиц. Но многолетние были споры о том, может ли диван иметь большую площадь, привели к тому, что в 2018 году международная группа математиков предположили, что верхняя граница максимальной площади дивана составляет 2,37 единиц.
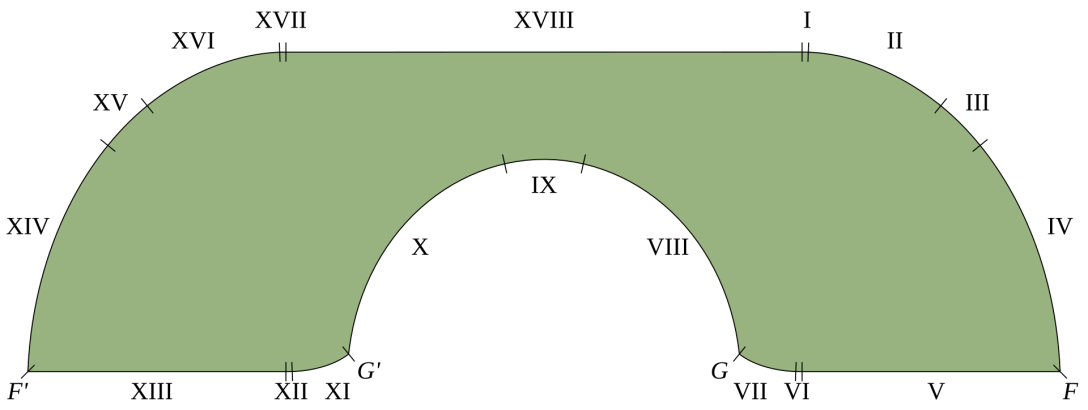
Так называемый «диван Гервера» является широким диваном, который немного напоминает латинскую букву U, имеет изогнутое сиденье и может переместиться в коридоре в форме буквы Г таким образом, что он не застревает. Вопрос заключался в том, имел ли этот диван, сделанный из 18 отдельных кривых, соединенных вместе, действительно самую большую и оптимальную форму для перемещения по коридору с прямым углом таким образом, чтобы сделать разворот. Бэк проработал геометрию формы этого дивана и его движение и обнаружил, что решение Гервера было, по сути, правильным.

Оставьте первый комментарий